Das getriebene Sinuspendel

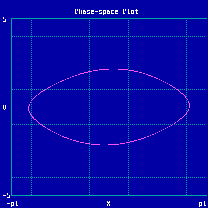
In der linearen Physik ist der getriebene gedämpfte Oszillator das Paradigma für Resonanzphänomene. Sein nichtlineares Analogon, das getriebene gedämpfte Sinuspendel zeigt ein weitaus reichhaltigeres dynamisches Verhalten. Bei mäßigen Amplituden ergibt sich im Phasenraum (x,v) eine einfach geschlossene Kurve, die noch an die elliptische Energiefläche des harmonischen Oszillators erinnert.

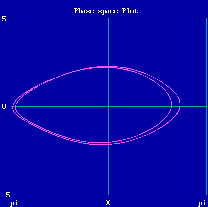Nähert sich die Amplitude dem instabilen Punkt (d.h. der kopfstehenden Pendellage) an, so kann es zur Periodenverdopplung kommen. In vielen dynamischen Systemen ist eine Serie von Periodenverdopplungen ein Weg zu chaotischen Zuständen.

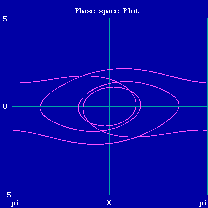Wenn die Amplitude weiter erhöht wird, besitzt das Sinuspendel neben der Vibrationsbewegung im Intervall (-180^o,180^o) auch die Möglichlkeit zur Rotation. Die Abbildung zeigt die Phasenraumtrajektorie für einen periodischen gemischten Zustand aus Vibration und Rotation.

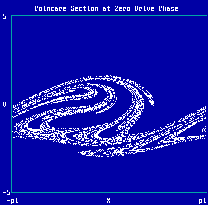Außer periodischen Zuständen finden sich bei großen Amplituden auch chaotische Zustände, für die die Phasenraumtrajektorie die (x,v)-Ebene scheinbar ausfüllt. Eine bessere Einsicht in diese chaotische Dynamik erhält man, indem man von der Trajektorie nur jeweils den Punkt darstellt, der einem festen Phasenwinkel (z.B. 0^o) des Treibersignals entspricht. Diese stroboskopische Darstellung ist topologisch gleichwertig zu einem Poincaré-Schnitt durch die Phasenraumtrajektorie. Das Beispiel zeigt, daß sich eine fraktale Punktmenge ergibt.

• Die Beispiele wurden mit dem Programm Chaos-Demostrations von Clint Sprott erstellt.
• Das Freeware-Programm Fractint erzeugt viele Standardbeispiele, u.a. die Mandelbrotmenge (mit Zoom-Funktion !), das Lorenz-System, die logistische Abbildung etc. Sehr zu empfehlen!
• Eine Shockwave Animation zum Schmetterlingseffekt