Diskrete Dynamik
Die Einsicht, daß simple mathematische Modelle äußerst komplexes
Verhalten erzeugen können, geht auf Robert May zurück, der sich mit der
Populationsdynamik beschäftigte. Das einfachste Modell, die
logistische Abbildung
beschreibt die Entwicklung nichtüberlappender Generationen einer Spezies
(z.B. Hasen) in einem Habitat (z.B. einem Kohlfeld).
Sei xn die Größe der Population in der Generation n, normiert
auf die maximale Größe der Population. Dann ist die nachfolgende Generation gegeben
durch
xn+1 = r xn (1 - xn)
Offensichtlich ist die Zahl der Nachkommen proportional zur Zahl der Eltern.
Daneben beschreibt der Faktor in der Klammer die verbliebenen Ressourcen
des Lebensraums. Wenn die Population den Maximalwert erreicht, erschöpfen sich die
Ressourcen und die nächste Generation ist klein infolge Verhungerns.
 |
Die Iteration zeigt die Entwicklung auf eine stabile Populationsgröße hin,
die einen Fixpunkt der Periode 1 darstellt. |
 |
Bei erhöhtem Kontrollparameter r
wird der ursprünglich stabile Fixpunkt am Schnittpunkt des Funktionsgraphen
mit der Identitätsfunktion instabil und es
ergibt sich eine Periodenverdopplung und die Population
schwankt zwischen zwei verschiedenen Werten. |
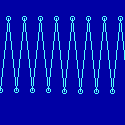 |
Die Zeitreihe zeigt die Periodizität 2.
Weitere Erhöhung von r erzeugt die Perioden 4 (Bild), 8, 16 usw.
in rasch zunehmender Sequenz |
 |
Trägt man die die Werte, die die Iteration der logistischen Abbildung nach Abklingen von
anfänglichen Transienten annimmt, für jeden Wert des Kontrollparameters r
auf der vertikalen Achse als Punkte auf, so erhält man das
Bifurkationsdiagramm. Hierin erkennt man die Folge von Periodenverdopplungen,
die in einem chaotischen Zustand enden. Der Bereich des Chaos ist durchsetzt mit
Fenstern, in denen ein periodischer zustand erscheint, der selbst
wiederum Periodenverdopplungen unterliegt. |
|